Confidence Intervals

Author

Jose Toledo Luna

last updated

November 7, 2023

Required Packages

library(ggplot2)
library(patchwork)
library(openintro)

theme_set(theme_bw())
theme_replace(panel.grid.minor = element_blank(),
              panel.grid.major = element_blank())

Confidence intervals provide a range of values that indicates the level of uncertainty associated with an estimate. This helps us understand the precision of the estimate, as apposed to a point estimate.

Show Code

generate_CI <- function(sample_size,n_samples,
                        population_size=1000,
                        critical_value = 1.96){

  population <- rnorm(population_size)
  sample_means <- replicate(n_samples, mean(sample(population,sample_size)))
  
  lower <- sample_means - critical_value * sd(population)/sqrt(sample_size)
  upper <- sample_means + critical_value * sd(population)/sqrt(sample_size)
  
  trial <- 1:n_samples
  cover <- (mean(population) >= lower) & (mean(population) <= upper)
  CIs <- data.frame(sample = trial, lower, upper, cover, n_samples)
  
  plt <- ggplot(CIs, aes(y = trial)) +
    geom_segment(aes(x=lower, y=trial, xend=upper, yend=trial, color= cover), 
                 show.legend=FALSE) +
    scale_color_manual(values=c('#bf0202','#ccecf0'))+
    annotate("segment", x=mean(population), xend=mean(population),
             y=0, yend=length(trial)+1, color="black",
             linewidth = 1,linetype =2) +
    labs(x=expression(bar(x)), y = "Iteration",
         title = paste0(100*mean(CIs$cover),'% ','coverage'))
  
  return(plt+facet_grid(~n_samples))
}
set.seed(90)
plt <- generate_CI(sample_size = 25, n_samples = 100)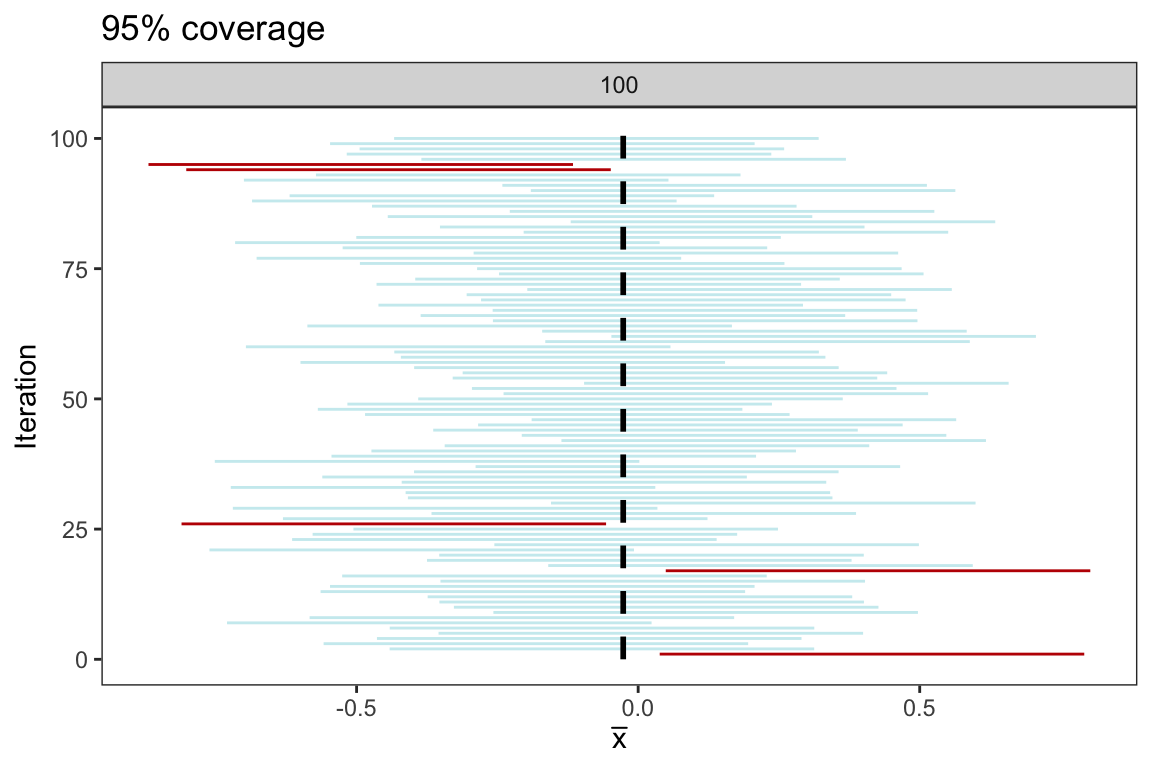

From the plot above, we see that 95 of the 100 confidence intervals cover the population parameter \(\mu = 0\). While it’s important to note that if we were to repeat the simulation another 100 times, the precise count may vary, but it is highly probable that it will remain close to 95

In the below plots, we repeat the same process mentioned above but this time constructing intervals from 100, 500, and 1000 samples each of size 25. The coverage percentage is demonstrated in the title of each respective plot

Show Code

plots <- generate_CI(sample_size = 25, n_samples = 100)+
  generate_CI(sample_size = 25, n_samples = 500)+
  generate_CI(sample_size = 25, n_samples = 1000)+
  plot_layout(ncol=3)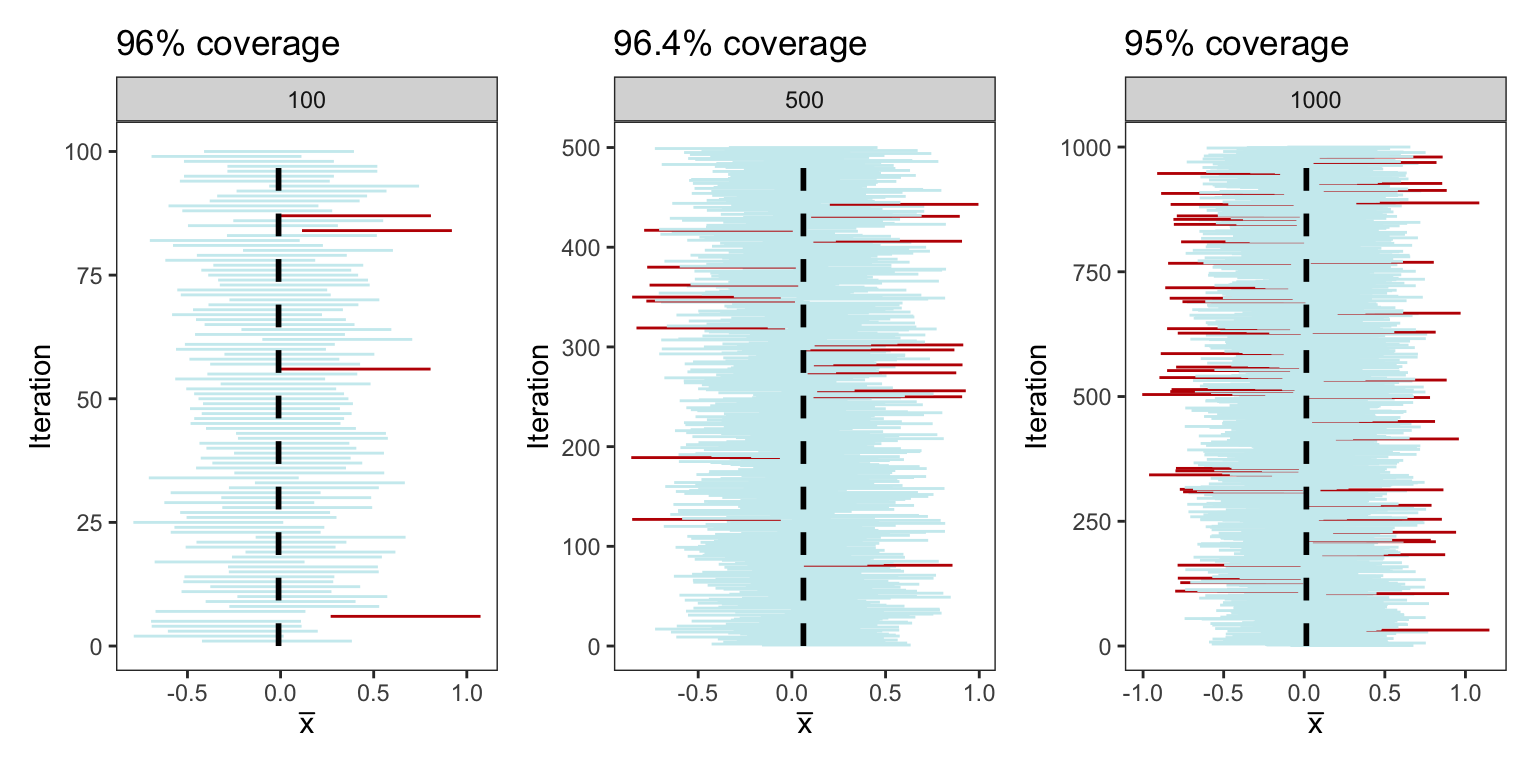

Inference for a Population Mean

We consider the Starbucks data set from the package openintro. This data gives nutrition facts for several food items at Starbucks, we are primarily interested in the average calories in the their food items.

starbucks <- openintro::starbucks

#> # A tibble: 6 × 7
#>   item                        calories   fat  carb fiber protein type  
#>   <chr>                          <int> <dbl> <int> <int>   <int> <fct> 
#> 1 8-Grain Roll                     350     8    67     5      10 bakery
#> 2 Apple Bran Muffin                350     9    64     7       6 bakery
#> 3 Apple Fritter                    420    20    59     0       5 bakery
#> 4 Banana Nut Loaf                  490    19    75     4       7 bakery
#> 5 Birthday Cake Mini Doughnut      130     6    17     0       0 bakery
#> 6 Blueberry Oat Bar                370    14    47     5       6 bakery

We create the sampling distribution for the sample proportion of tenured professors and compare it to the population distribution of all the professors ranks

n_samples <- 10000
sample_size <- 30
calories <- starbucks$calories
sample_calories <- numeric(n_samples)

for(i in 1:n_samples){
  sample_i =  sample(calories, size = sample_size) # generate a new sample from the population
  sample_calories[i] = mean(sample_i) # obtain proportion for each sample
}

Show Code

pop_plt <- ggplot(starbucks) +
 geom_histogram(mapping = aes(x = calories), bins = 30,
          fill='steelblue',alpha = 0.3,color='black')+
  labs(title = 'Population Distribution',
       subtitle= "Calories of Food",
       y = 'Counts', x = 'Calories')

sampling_dist <- ggplot(data.frame(sample_calories),
                        aes(sample_calories))+
  geom_histogram(fill = 'steelblue',alpha = 0.3,bins = 30,
                 color = 'black')+
  labs(title = 'Sampling distribution of Sample Mean',
       subtitle = "Calories of Food",
       x = 'Calories',y = '')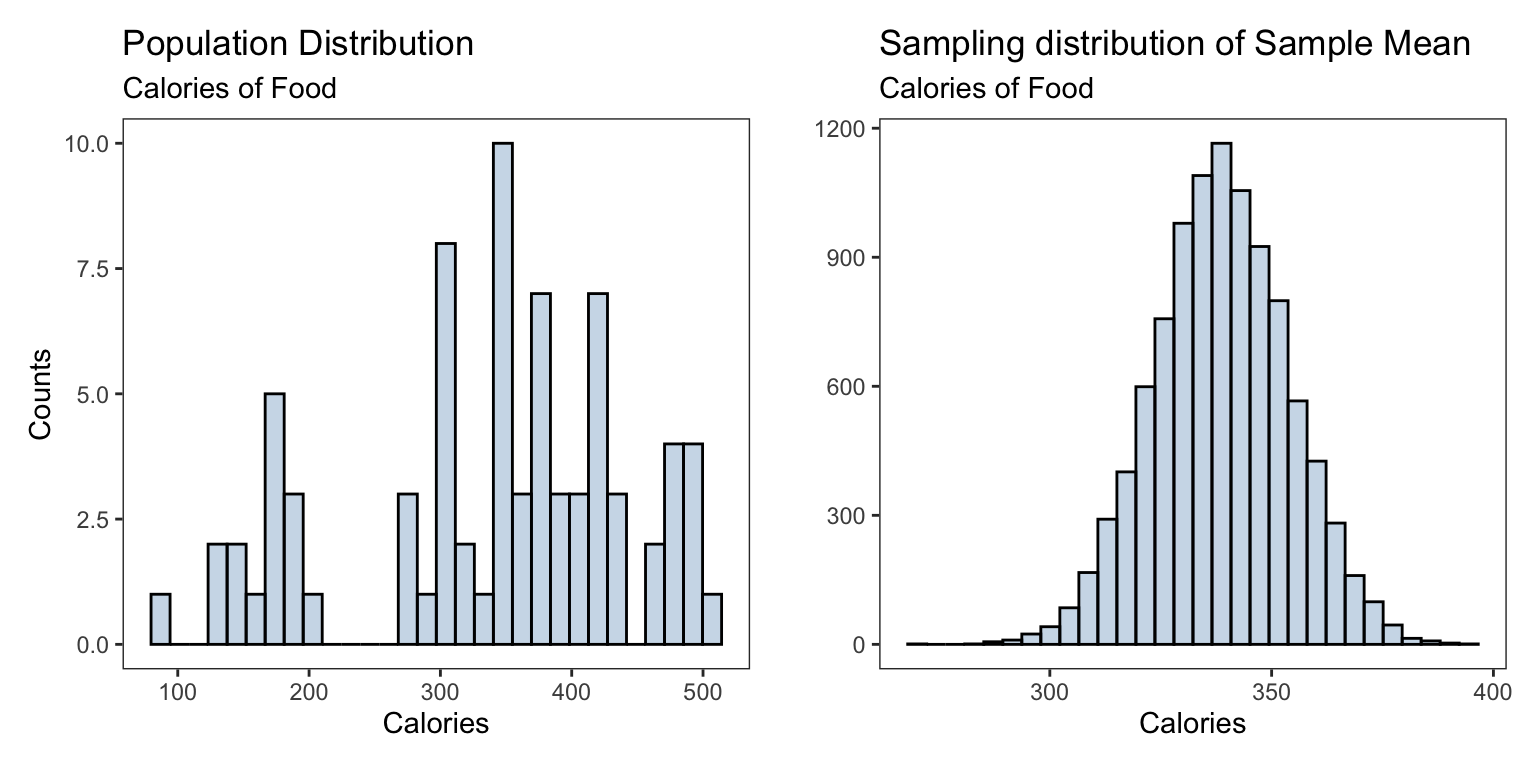

	Population	Sampling
Shape	skewed	normal/bell-shaped
Mean	338.8311688	338.6314
SD	\(\sigma =\) 105.3687014	\(\frac{\sigma}{\sqrt{n}} =\) 19.2376049

When the sampling distribution is roughly normal in shape, then we can construct an interval that expresses exactly how much sampling variability there is. Using our single sample of data and the properties of the normal distribution, we can be 95% confident that the population parameter is within the following interval \[ \left[\overline{x} - ME \, \, , \, \,\overline{x} + 1.96 ME \right] \]

where the margin of error \(ME = \text{critical value} \times SE\). The critical value for a \(100(1-\alpha\))% CI can be obtained by qnorm(p = 1-alpha/2) whenever the sample size is large enough, say \(n=30\) and the sampling distribution is approximately normal (bell-shaped)

For example, a 90% = 100(1-0.1)% CI can be calculated as

alpha = 0.1
qnorm(p = 1-alpha/2)

#> [1] 1.644854

Commonly used critical values are

Confidence Level	Critical Value	R code
99%	2.58	`qnorm(p = 1-0.01/2)`
95%	1.96	`qnorm(p = 1-0.05/2)`
90%	1.65	`qnorm(p = 1-0.1/2)`

The standard error can be approximated using \(SE = \frac{\sigma}{\sqrt{n}} \approx \frac{s}{\sqrt{n}}\), where \(s\) is the standard deviation of the sample obtained from the population

Putting all of this together, a 95% CI is \[ \left[\overline{x} - 1.96 \frac{s}{\sqrt{n}} \, \, , \, \, \overline{x} + 1.96 \frac{s}{\sqrt{n}} \right] \]

set.seed(1)
sample_calories <- sample(calories, 30)
xbar_calories <- mean(sample_calories)
sd_calories <- sd(sample_calories)

For our Starbucks calories example, A sample mean obtain from a SRS is \(\overline{x} =\) 353.333 and standard deviation \(s=\) 90.984 then the 95% CI is

lower_bound <- xbar_calories - 1.96*(sd_calories/sqrt(30))
upper_bound <- xbar_calories + 1.96*(sd_calories/sqrt(30))

c(lower_bound, upper_bound)

#> [1] 320.7750 385.8917

We are 95% confident the population avarage for calories of food at Starbucks is between 320.775 and 385.892

Inference for a Population Proportion

We consider the Professor evaluations and beauty data from the package openintro. This data was gathered from end of semester student evaluations for 463 courses taught by a sample of 94 professors from the University of Texas at Austin. In addition, six students rate the professors’ physical appearance. The result is a data frame where each row contains a different course and each column has information on the course and the professor who taught that course

professor_evaluations <- openintro::evals

#> # A tibble: 6 × 23
#>   course_id prof_id score rank     ethnicity gender language   age cls_perc_eval
#>       <int>   <int> <dbl> <fct>    <fct>     <fct>  <fct>    <int>         <dbl>
#> 1         1       1   4.7 tenure … minority  female english     36          55.8
#> 2         2       1   4.1 tenure … minority  female english     36          68.8
#> 3         3       1   3.9 tenure … minority  female english     36          60.8
#> 4         4       1   4.8 tenure … minority  female english     36          62.6
#> 5         5       2   4.6 tenured  not mino… male   english     59          85  
#> 6         6       2   4.3 tenured  not mino… male   english     59          87.5
#> # ℹ 14 more variables: cls_did_eval <int>, cls_students <int>, cls_level <fct>,
#> #   cls_profs <fct>, cls_credits <fct>, bty_f1lower <int>, bty_f1upper <int>,
#> #   bty_f2upper <int>, bty_m1lower <int>, bty_m1upper <int>, bty_m2upper <int>,
#> #   bty_avg <dbl>, pic_outfit <fct>, pic_color <fct>

We are interested in the proportion of professors who are of rank “Tenured”. The proportions of the professors ranks are shown below

table(professor_evaluations$rank) |> 
  prop.table()

#> 
#>     teaching tenure track      tenured 
#>    0.2203024    0.2332613    0.5464363

We create the sampling distribution for the sample proportion of tenured professors and compare it to the population distribution of all the professors ranks

n_samples <- 10000
sample_size <- 50
rank_proportions <- numeric(n_samples)

for(i in 1:n_samples){
  sample_i =  sample(professor_evaluations$rank, size = sample_size) # generate a new sample from the population
  rank_proportions[i] = mean(sample_i == 'tenured') # obtain proportion for each sample
}

Show Code

sampling_dist <- ggplot(data.frame(rank_proportions),
                        aes(rank_proportions))+
  geom_bar(fill = 'steelblue',alpha = 0.3,
                 color = 'black')+
  labs(title = 'Sampling distribution of Sample Proportion',
       subtitle = "Professor Ranks",
       x = 'Proportion of Tenured',y = '')

pop_plt <- ggplot(professor_evaluations) +
 geom_bar(mapping = aes(x = rank, y = ..prop.., group = 1), stat = "count",
          fill='steelblue',alpha = 0.3,color='black')+
  labs(title = 'Population Distribution',
       subtitle= "Professor Ranks",
       y = 'Proportion', x = 'Rank')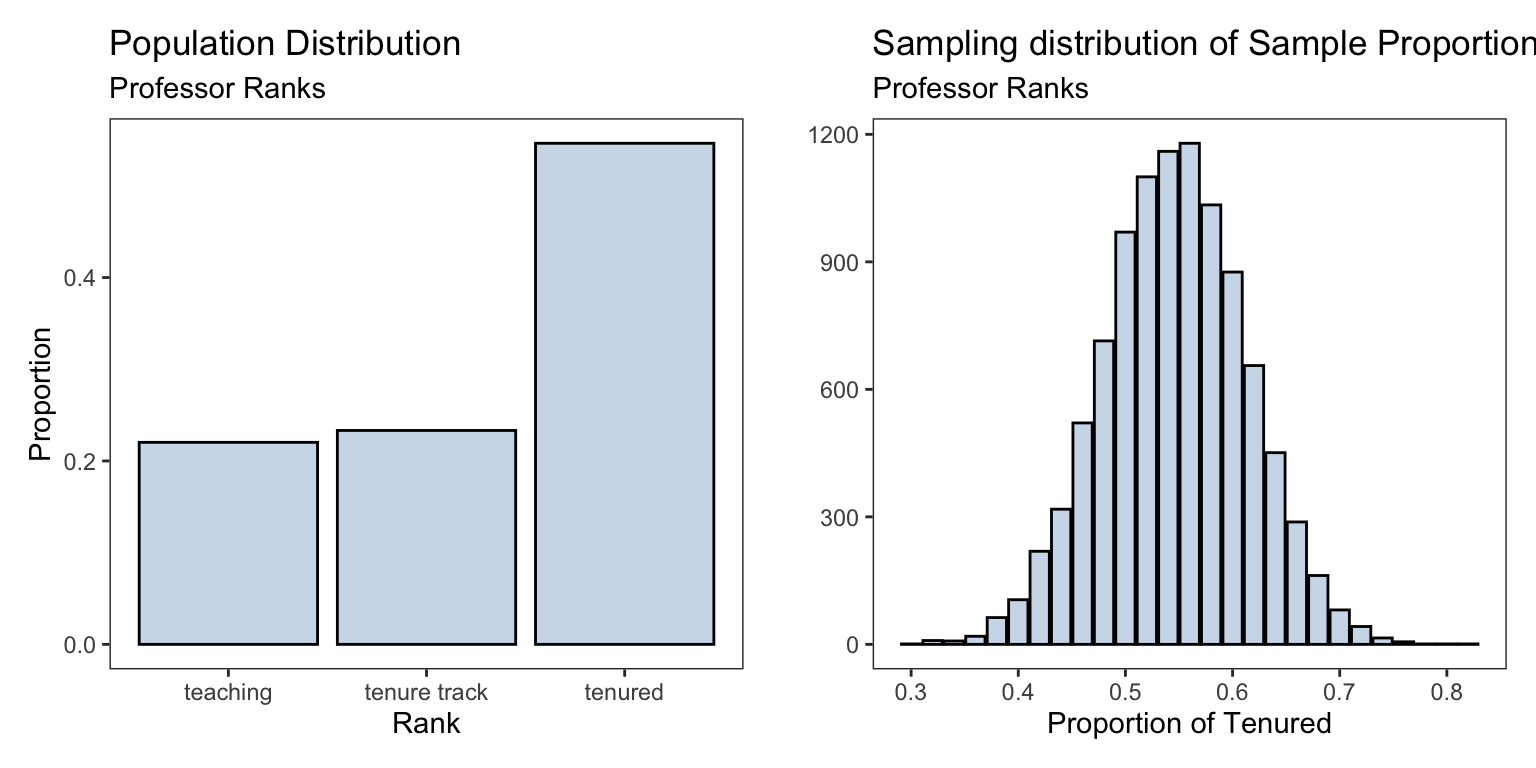

	Population	Sampling
Shape		normal/bell-shaped
Mean	\(p=\) 0.5464363	\(\hat{p}=\) 0.546252
SD	\(\sigma = \sqrt{p(1-p)} =\) 0.497839	\(\sqrt{\frac{p(1-p)}{n}} =\) 0.0704075

We can form a 95% confidence interval for the population proportion of professors who are tenured rank at the University of Texas at Austin \[ \left( \hat{p} - \, 1.96 \sqrt{\frac{\hat{p}(1-\hat{p})}{n}} \, \, , \quad \hat{p}+ \, 1.96 \sqrt{\frac{\hat{p}(1-\hat{p})}{n}} \right) \]

Giving us the following 95% CI (0.408,0.684). We can see the constructed interval contains the population proportion of 0.5464363. A simple interpretation of this confidence interval is

We are 95% confident that the population proportion of tenured professors at the University of Texas is between 0.408 and 0.684