library(openintro)Theory-Based Test of Significance
Required Packages
Hypothesis tests
There are a few components common to every hypothesis test
Null Hypothesis
A hypothesis that posits there is no significant difference, effect, or relationship in the variables being studied. Suggesting any observed differences are due to random chance Denoted by \(H_0\) (“H naught”)
Alternative Hypothesis
A hypothesis that contradicts the null hypothesis, proposing that there is a significant difference, effect, or relationship in the variables being studied, beyond what could be explained by random chance. Denoted by \(H_a\)
Test Statistic
A numerical value calculated from sample data used to assess the strength of the evidence against the null hypothesis, with larger values indicating stronger evidence in favor of the alternative hypothesis
p-value
The probability of a test statistic as rare or even more rare than the one observed under the assumptions of the null hypothesis
The p-value quantifies the likelihood of observing the data or more extreme results under the null hypothesis; a lower p-value indicates that the observed statistic is highly improbable under the null hypothesis, strengthening the evidence against it and often leading to its rejection in favor of the alternative hypothesis
One Sample \(t\)-test
To perform a theory-based hypothesis test for the mean of a quantitative variable, following the components of a hypothesis test, but in the context of a one sample \(t\)-test
State the null and alternative hypotheses about the mean parameter \(\mu\)
From a sample of data, compute the sample mean \(\bar{x}\) and its standardized \(t\)-statistic
Check the validity conditions to apply the Central Limit Theorem
If the validity conditions hold, compute the \(p\)-value by comparing the observed \(t\)-statistic to a \(t\)-distribution with \(df = n-1\)
We can use the t.test() function to conduct this hypothesis test
The basic syntax for the t.test() function is as follows:
t.test(x, y = NULL,
alternative = c("two.sided", "less", "greater"),
mu = 0, conf.level = 0.95, ...)x: numeric vector of data values (our sample)y: an optional numeric vector of data values (response)alternative: type of hypothesis being performed,"two.sided": \(H_a: \mu \neq \mu_0\)"less": \(H_a: \mu < \mu_0\)"greater": \(H_a: \mu > \mu_0\)
mu: population mean \(\mu\) (null value), can be difference of means if performing a two-sample testconf.level: confidence level of the interval \(100(1-\alpha)\)%, where \(\alpha\) is the significance level
For additional arguments ... see ?t.test()
Consider the Tip Data from opentintro package. The tip data is a simulated data set of tips over a few weeks on a couple days per week. Each tip is associated with a single group, which may include several bills and tables
From this dataset we obtain a simple random sample of 30 tips, but first we only consider tips from bills that were at most $80
tips <- openintro::tips#> Rows: 95
#> Columns: 5
#> $ week <int> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, …
#> $ day <fct> Tuesday, Tuesday, Tuesday, Tuesday, Tuesday, Tuesday, Tuesday, …
#> $ n_peop <dbl> 0.67, 1.33, 5.33, 2.67, 1.33, 2.00, 1.33, 2.67, 2.00, 1.33, 1.3…
#> $ bill <dbl> 17.99, 26.05, 79.49, 32.69, 29.97, 23.91, 18.18, 41.23, 25.19, …
#> $ tip <dbl> 2.0000, 4.0000, 14.3082, 5.5000, 6.0000, 7.5000, 3.0600, 8.5000…tips_bill_at_most80 <- tips[tips$bill <= 80,]Among the tips from bills that were at most $80, we obtained a simple random sample of size 30. We are interested in determining if the average tips throughout the weeks will be greater than $5 per group (for some reason, the business needs on average at least $5 tips per group to stay in business).
The null and alternative hypothesis are given by \[ \begin{align*} H_0: \mu = 5 \\[5pt] H_a: \mu > 5 \end{align*} \]
set.seed(1234)
rows_sample <- sample(1:nrow(tips_bill_at_most80), 30)
tips_sample <- tips_bill_at_most80[rows_sample,]First we will carry out a one-sample \(t\)-test the long way. First, we compute the sample mean for the tips
x_bar <- mean(tips_sample$tip)
x_bar#> [1] 6.533687Next, compute the sample standard deviation of the tips
s <- sd(tips_sample$tip)the \(t\)-statistic is then computed as
\[ t = \frac{\bar{x}-\mu_0}{\left(\frac{s}{\sqrt{n}} \right)} \]
n <- length(rows_sample)
mu_0 <- 5
t_stat <- (x_bar - mu_0) / (s / sqrt(n))t_stat#> [1] 1.74364Lastly, obtain the \(p\)-value
p_value <- pt(t_stat, df = n - 1,lower.tail = FALSE)p_value#> [1] 0.0459079At a significance level of \(\alpha=0.05\), we reject the null hypothesis, indicating there is enough evidence to propose that, on average, the tips per group exceed $5 for bills equal to or less than $80, as supported by the three-week data provided
With a single command, we can use t.test() function and obtain all of the following information, without having to compute every step ourselves
- observed sample mean \(\bar{x}\)
- \(t\)-statistic
- degrees of freedom \((df)\)
- the alternative hypothesis we are testing
- \(p\)-value
- A 95% confidence interval for \(\mu\)
t.test(tips_sample$tip, mu=5,
alternative = 'greater')#>
#> One Sample t-test
#>
#> data: tips_sample$tip
#> t = 1.7436, df = 29, p-value = 0.04591
#> alternative hypothesis: true mean is greater than 5
#> 95 percent confidence interval:
#> 5.039153 Inf
#> sample estimates:
#> mean of x
#> 6.533687Two Sample \(t\)-test
To perform a theory-based hypothesis test for the mean of a quantitative variable, following the components of a hypothesis test, but in the context of a two sample \(t\)-test
State the null and alternative hypotheses about the difference in mean parameters \(\mu_1 - \mu_2\)
From a sample of data, compute the difference in sample means \(\bar{x}_1 - \bar{x}_2\) and its standardized \(t\)-statistic
Check the validity conditions to apply the Central Limit Theorem
If the validity conditions hold, compute the \(p\)-value by comparing the observed \(t\)-statistic to a \(t\)-distribution with \(df=n_1+n_2-2\) or \(df\) obtained by Welch \(t\)-statistic if the variances of the two groups are different
Continuing with the tips dataset, we are now interested in determining if the average tips obtained on Friday are greater than those on Tuesday. Our null and alternative hypothesis are \[
\begin{align*}
H_0: \mu_{friday} &= \mu_{tuesday} \\[10pt]
H_a: \mu_{friday} &> \mu_{friday}
\end{align*}
\]
tips_friday <- tips_bill_at_most80$tip[tips_bill_at_most80$day=='Friday']
tips_tuesday <- tips_bill_at_most80$tip[tips_bill_at_most80$day=='Tuesday']boxplot(tips_tuesday,tips_friday,
names = c('Tuesday','Friday'),
col=c('#f5d376','#f5767c'),
main = 'Tips by Day',
ylab = 'Tips ($)')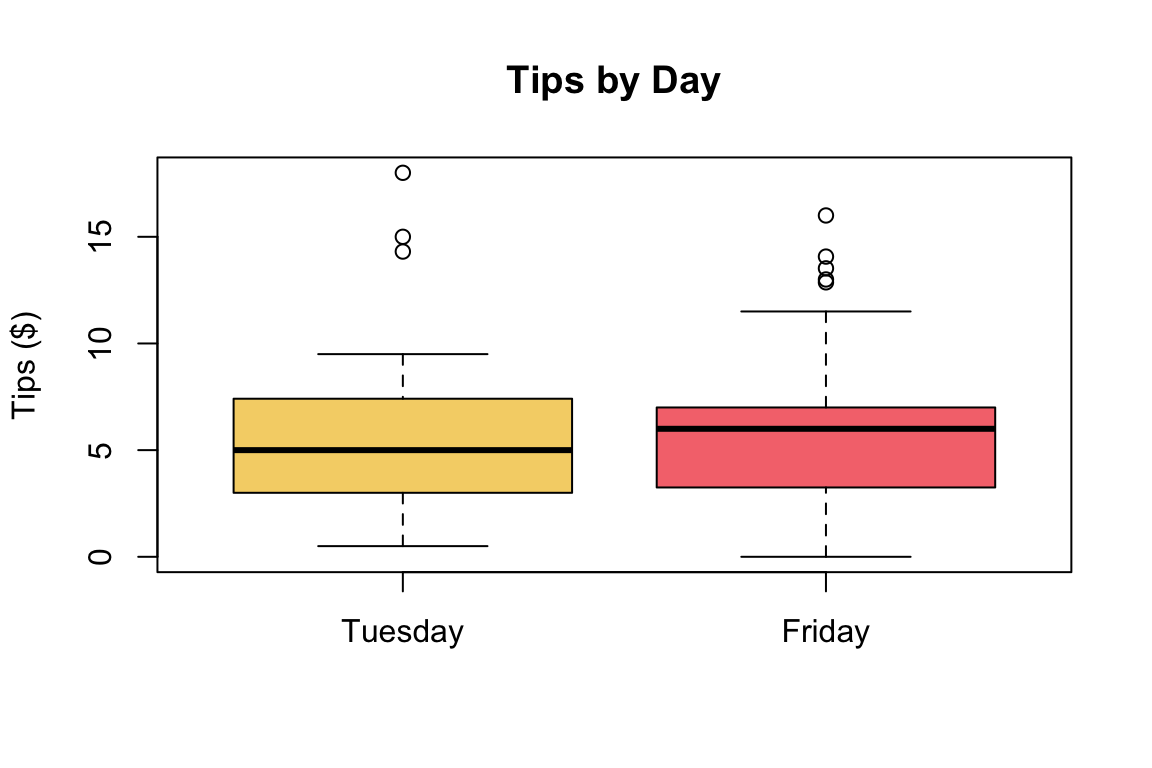
Show Derivations
sample_sizes <- table(tips_sample$day)
sample_sizes#>
#> Friday Tuesday
#> 16 14Here \(n_1 = 16\) and \(n_2 = 14\)
The sample means for the respective day based on our sample are given below
sample_means <- tapply(tips_sample$tip,tips_sample$day,"mean")
sample_means#> Friday Tuesday
#> 6.372025 6.718443where \(\bar{x}_1 =\) 6.372 and \(\bar{x}_2 =\) 6.718 their difference is then \(\bar{x}_1 - \bar{x}_2=\) -0.346. This will be our test statistic.
The respective standard deviations can be computed in a similar manner
sample_sd <- tapply(tips_sample$tip,tips_sample$day,"sd")
sample_sd#> Friday Tuesday
#> 4.482114 5.341150Therefore, \(s_1 =\) 4.482 and \(s_2=\) 5.341
The standardized test statistic is \[ t = \frac{(\bar{x}_1 - \bar{x}_2)- (\mu_1 - \mu_2)}{\sqrt{\frac{s_1^2}{n_1} + \frac{s_2^2}{n_2}} } \]
Plugging in all the computed values from earlier, we can then compute the standardized \(t\)-statistic
numerator <- (sample_means[1]-sample_means[2])
denominator <- sqrt(sample_sd[1]^2/sample_sizes[1] +
sample_sd[2]^2/sample_sizes[2])
t_stat <- numerator/denominatort_stat#> Friday
#> -0.1908909the degrees of freedom of Welch \(t\)-test is estimated as follows \[ df = \left(\frac{s_1^2}{n_1} + \frac{s_2^2}{n_2}\right)^2 \Big/ \left(\frac{s_1^2}{n_1(n_1-1)} + \frac{s_2^2}{n_2(n_2-1)} \right) \]
v_1 <- sample_sd[1]^2/sample_sizes[1]
v_2 <- sample_sd[2]^2/sample_sizes[2]df_numerator <- (v_1 + v_2)^2
df_denominator <- (1/(sample_sizes[1]-1))*(v_1^2) + (1/(sample_sizes[2]-1))*(v_2^2)
df <- df_numerator/df_denominator
df#> Friday
#> 25.54932Lastly, obtain the \(p\)-value
p_value <- pt(t_stat, df = df,
lower.tail = FALSE)p_value#> Friday
#> 0.5749401Without all the complicated procedure of carrying a two sample \(t\)-test, we can simply use the t.test() function like we did in the one sample \(t\)-test scenario
This time the input will be a formula y ~ x where \(y\) is the response of interest and \(x\) is the group, in our case we are interested in the average tips by day so our input would be tip ~ day
t.test(tip ~ day, data = tips_sample, var.equal = FALSE,
alternative = 'greater')#>
#> Welch Two Sample t-test
#>
#> data: tip by day
#> t = -0.19089, df = 25.549, p-value = 0.5749
#> alternative hypothesis: true difference in means between group Friday and group Tuesday is greater than 0
#> 95 percent confidence interval:
#> -3.443692 Inf
#> sample estimates:
#> mean in group Friday mean in group Tuesday
#> 6.372025 6.718443Since the \(p\)-value is greater than our significance level \(\alpha = 0.05\) we do not have sufficient evidence to suggest the average tips on Friday are greater than that of Tuesday